莫队算法(离线统计区间)

发表于 | 分类于 |

久仰大名的莫队算法

首先，给定一个长度为n的数列，给定m个[L,R]的询问，给出[L,R]区间上的不同数字个数

1.暴力做法：对每次询问暴力遍历区间，时间复杂度为O(m*n)

2.暴力改良:用双指针(或者说滑动窗口?）+离线做法，对每个询问区间进行排序，通过移动L、R进行更新信息（cnt[i]表示i的个数，i降为0时ans-1，i升为1时，ans+1）

然而，排序不当的情况下复杂度会退化成n*n级

问题：如何排序区间使复杂度小？

图中x表示L，y表示R，而点与点之间的转移其实就是区间的转移，操作次数是两点之间的曼哈顿距离，而我们希望找到连接若干个点的Hamilton最短路径（然而这是个NP问题==）

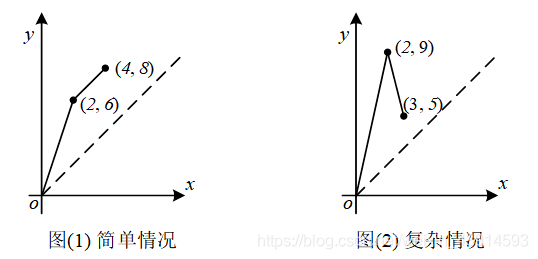
3.莫队算法：实际上，莫队算法就是上述双指针暴力法引入了排序方法

我们将1~n分为根号n块，将所有的区间按以下规则排序：

1.首先按L所在块的序号排序

2.L所在块序号相同时，按R的序号排序

优化后，点的连接如下：

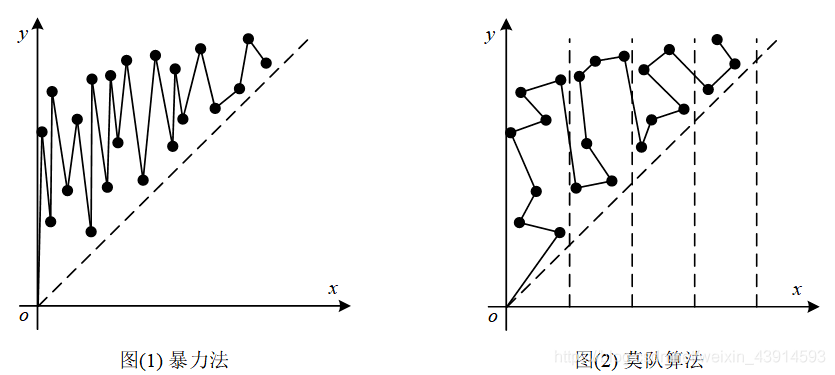
实际上是将点分为了根号n块

则x方向上，一次最多移动根号n，一共移动m次，故复杂度为O（m*sqrt(n))

y方向上，在一个块内，沿y方向一共移动n，共有sqrt(n)个区间，故复杂度为O(n*sqrt(n))

综上，总距离为O((m+n)*sqrt(n))

结合图，我们还可看出一个优化方法：当块的序号为奇数时，从大到小排，当块的序号为偶数时，从小到大排，这样在跨越区间的移动时，能使距离更小

例题:https://www.luogu.com.cn/problem/P2709

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<vector>
#include<string>
#include<map>
#include<cstdio>
#include<list>
#include<stack>
#include<deque>;
#include<unordered_set>
using namespace std;
using ll = long long;
ll T;
ll n;
ll m, k;
ll a[100005];
ll now[100005];
ll c;
struct query
{
	ll ql, qr, qc;
	ll id;
	ll ans;
}q[100005];
ll be[100005];
bool cmp1(query a, query b)
{
	if (be[a.ql] == be[b.ql])
	{
		if (be[a.ql] % 2)
		{
			return a.qr < b.qr;
		}
		return b.qr < a.qr;
	}
	return be[a.ql] < be[b.ql];
}
bool cmp2(query a, query b)
{
	return a.id < b.id;
}
void add(ll x)
{
	
	c -= now[a[x]]*now[a[x]];
	now[a[x]]++;
	c += now[a[x]] * now[a[x]];
}
void del(ll x)
{
	c -= now[a[x]] * now[a[x]];
	now[a[x]]--;
	c += now[a[x]] * now[a[x]];
}
int main()
{
	cin.tie(0);
	ios::sync_with_stdio(false);
	cin >> n >> m >> k;
	c = 0;
	memset(now, 0, sizeof(now));
	for (ll i = n; i>=1; i--)
	{
		be[i] = i << 8;
	}
	for (ll i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	for (ll i = 1; i <= m; i++)
	{
		cin >> q[i].ql >> q[i].qr;
		q[i].id = i;
	}
	sort(q+1, q + 1 + m, cmp1);
	ll l = 1, r = 0;
	for (ll i = 1; i <= m; i++)
	{
		while (l < q[i].ql)
		{
			del(l++);
		}
		while (l > q[i].ql)
		{
			add(--l);
		}
		while (r < q[i].qr)
		{
			add(++r);
		}
		while (r > q[i].qr)
		{
			del(r--);
		}
		q[i].ans = c;
	}
	sort(q + 1, q + 1 + m, cmp2);
	for (ll i = 1; i <= m; i++)
	{
		cout << q[i].ans << '\n';
	}
	return 0;
}

该code注意：

初始化l=1，r=0

add先移再算，del先算再移

莫队适用条件:无修改、可离线、基于分块

若加入修改？

对询问引入时间指针t，表示在第t个修改之后的询问

与之前l、r的排序类似，只有当l、r所在分块均相同时，依据t的大小排序。而与移动l、r指针的操作类似，我们对时间指针进行移动。用坐标来联想的话，是一个三维坐标

我们开始分析时间复杂度：假设询问次数、修改次数、区间长度都为n，块的区间长度为

L指针：

  1. L指针在块内移动，最多移动次,最多n次，故块内移动的是
  2. L指针在块间移动，最多移动,最多次，故块间移动的复杂度是

R指针：

  1. L指针在块内移动，R指针移动总次数最多为次，一共有块，故一共移动
  2. L指针在块间移动，R指针最多移动次，一共有次，故时间复杂度为

T指针:

  1. L指针、R指针均在块内，T指针总移动次数最多为,一共有个块，故总复杂度为
  2. L指针在块内，R指针在块间移动，T指针移动次数最多为，最多移动次，故总复杂度为
  3. L指针、R指针均在块间移动，T指针最多移动,最多移动次，故总复杂度为次

综上，最后的复杂度为，使其最小时，取,此时复杂度为。