学一下Polya,能不能学会就看命了()
来抛一个引入问题:https://acm.hdu.edu.cn/showproblem.php?pid=6960
有k个绿珠子,无穷个红珠子和蓝珠子,要串出环状项链,规定相邻珠子不同色,两种项链可以通过旋转得到,则认为是同一种项链,求有多少种项链(T=10,n<=1e6,k<=1e6)
首先,复习一下置换群的概念,集合S上的所有置换均满足有逆元,有单位元,结合律(a*b*c=a*(b*c)),因此我们称其为一个群,而该群的任意一个子群都称为置换群
然后看一下循环置换,顾名思义,就是a1a2a3变成a2a3a1的置换(),我们可以将任意的置换替换成若干个不相交的循环置换的乘积(非常显然,若a1被映射成a2,我们接着去找a2被映射成什么,就形成了一个a1—a2—???….的映射环,其中前一个节点被映射成后一个节点,而该映射环其实就是一个循环置换)
然后预习一下Burnside定理(对不起我的组合数学老师,这个我是真没学orz)
总之就是直接上结论了,对所有置换/翻转的方式,保持不变的方案数的和,除以所有置换方式的总数
套入一个经典例子,就是给正方体的6个面染色,对于绕两个对面中心连线180度旋转的方式,显然,中心一共有6/2=3种选择,而保持不变的要求是4个面都相同,则对特定中心的方案数是3^3,最后的方案数是3*3^3,而置换方式要+3
还需要注意,绕两个对面中心连线180度旋转和90度旋转,视作两种不同的旋转方式(因为二者显然不等价),而270度可以视作90度的旋转的等价(以置换的角度看,123456变成412356,和123456变成234156是等价的),360度同理
可以这么理解,置换方式即”旋转中心”数,而保持不变的方案数即置换方式*该置换方式下的不变方案数
最后来到了Polya定理,
显然,刚才计数保持不变的方案数时,我们可以将面看作(1,2,3,4,5,6),而旋转就是一个置换,我们将该置换拆解成循环置换,设拆解出的循环置换数为x(注意映射到自身,我们视其为长度为1的循环置换),则最终保持不变的方案数就是B^x(B为颜色数),很显然,一个循环置换内,其颜色都必须相同才能保证不变,故本质就是为x个循环置换挑选颜色.
然而大多数题都不会这么白板,经常会添加附加条件,这时候我们需要在计算不变方案数时下点功夫()
比如:https://www.luogu.com.cn/problem/P1446
由于有个颜色数量的限制,我们在为循环置换挑选颜色时,需要采用背包dp的方式
回到一开始引入的题目,我们现在可以尝试解决他了.显然,项链旋转可以看作是一个整体位移(长度为0~n-1),故我们知道置换方式一共有n种,假设确定位移长度为x的话,1映射成x+1,x+1映射成2x+1,2\x+1映射3*x+1,易知这个循环置换的长度为n/gcd(n,x).(prove: 假设循环置换的长度为k,则k是最小的正整数满足k*x%n=0,也就是n/gcd(n,x))
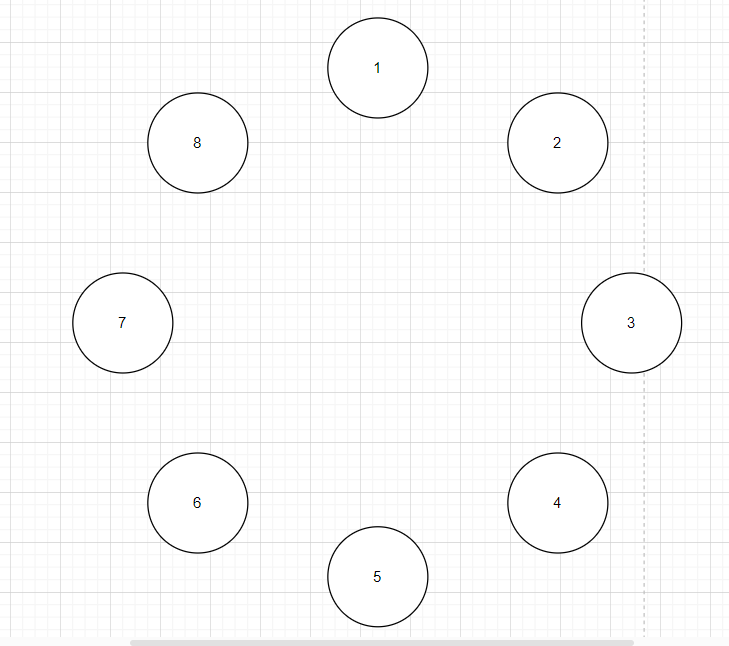
eg:
假设x为3,则对应的循环置换:
- 1-4-7-2-5-8-3-6-1
假设x为2,则对应的循环置换:
- 1-3-5-7-1
- 2-4-6-8-2
假设x为4,则对应的循环置换:
- 1-5-1
- 2-6-2
- 3-7-3
- 4-8-4
假设x为5,则对应的循环置换:
- 1-6-3-8-5-2-7-4-1
可以发现,最终的循环置换个数就是gcd(n,x),而每个循环置换可以用1~gcd(n,x)中的一个数表示(两个数之间的差若小于等于gcd(n,x),则二者不处于一个循环置换内—exgcd相关可得)
按照Burnside定理,我们将问题化简为,为每一个循环置换决定颜色,而由于题目的两个限制:1.绿色的珠子不超过k个;2.相邻珠子不同色.我们还需要在方案统计上下点功夫
显然,按照循环置换考虑,可以将绿色珠子不超过k个变成,选择绿色的循环置换数不超过k/(n/gcd(n,x))个,而观察我们得出的循环置换,由于环状结构和同一置换内颜色相同,我们可以将项链视作一个循环节重复n/gcd(n,x)次(即第一个置换—第二个置换—第三个置换—第四个置换—…—第一个置换)
显然,可以得出一个长度为置换个数的环,那么在这个环中挑选不超过k/(n/gcd(n,x))个绿色珠子的方案数,就等价于原问题中的不变方案数.
即
其中f(n,m)表示在长度为n的环中,挑选m个绿色珠子的合法方案(不需考虑置换等价问题)
显然,直接计算的复杂度过大,观察式子可以发现枚举i时,对答案计算有意义的仅是gcd(i,n),那么我们可以转为枚举gcd(i,n),计算由多少i满足gcd(i,n)为该值(这部分由欧拉函数就可得出),对每个gcd仅用枚举一次j